Tales de Mileto.

Era hijo de Euxamias y de Cleobulinas, ambos oriundos de Fenicia y descendientes de Cadmo y Agenor. Puesto que los jonios comerciaban frecuentemente con Egipto y Babilonia, es probable que Tales visitara Egipto en alguna etapa de su vida, y allí podría, por un lado, haber recibido enseñanzas de los sacerdotes, quienes registraban con mucho celo todo evento astronómico o meteorológico excepcional por motivos religiosos y que poseían, por consiguiente, copiosa información al respecto; y, por el otro, haber adquirido conocimientos matemáticos, que los egipcios habían desarrollado a un nivel práctico con el fin de medir y delimitar las parcelas de tierra cuyos límites solían borrarse con las continuas crecidas del río Nilo.
Obras
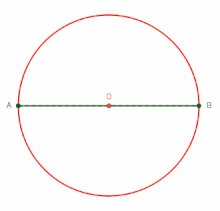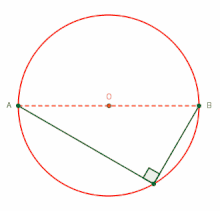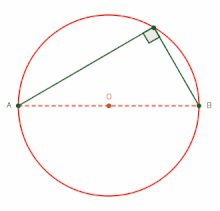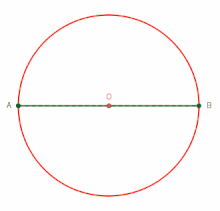
Teorema de Tales del ángulo inscrito
Simplicio de Cilicia escribió: «Se dice de Tales que no dejó nada escrito, excepto la llamada Astrología náutica .
En cambio Diógenes Laercio escribe: «Según algunos, nada dejó escrito, pues dicen que la Astrología náutica que se le atribuye es de Foco Samio [...] Pero, según otros, escribió dos obras: Sobre el solsticio y Sobre el equinoccio».7
Así, son tres las líneas de opinión: que solo escribió la Astrología, que solo escribió Sobre el solsticio y Sobre el equinoccio y que no escribió nada. De cualquier manera, lo cierto es que, de haber escrito algo, sus escritos se perdieron pronto, y, respecto de las pocas fuentes que citan presuntos dichos de Tales, no puede determinarse con certeza si tales fuentes tenían en sus manos o bien escritos de Tales o bien fuentes secundarias o si solo repetían tradiciones orales.
Aportes matemáticos
Se atribuyen a Tales varios descubrimientos matemáticos registrados en los Elementos de Euclides: la definición I. 17 y las proposiciones I. 5, I. 15, I. 26 y III. 31.
Los egipcios habían aplicado algunos de estos conocimientos para la división y parcelación de sus terrenos. Esta necesidad surgió a raíz de que el Nilo, con sus constantes crecidas, borraba las líneas divisorias de los campos de cultivo, por lo que era necesaria una manera de medir de nuevo el terreno. Mas, según los pocos datos con los que se cuenta, Tales se habría dedicado en Grecia mucho menos al espacio (a las superficies) y mucho más a las líneas y a las curvas, alcanzando así su geometría un mayor grado de complejidad y abstracción.
Aportes en el campo filosófico y cientifico

Teorema de Tales del ángulo inscrito
Simplicio de Cilicia escribió: «Se dice de Tales que no dejó nada escrito, excepto la llamada Astrología náutica .
En cambio Diógenes Laercio escribe: «Según algunos, nada dejó escrito, pues dicen que la Astrología náutica que se le atribuye es de Foco Samio [...] Pero, según otros, escribió dos obras: Sobre el solsticio y Sobre el equinoccio».7
Así, son tres las líneas de opinión: que solo escribió la Astrología, que solo escribió Sobre el solsticio y Sobre el equinoccio y que no escribió nada. De cualquier manera, lo cierto es que, de haber escrito algo, sus escritos se perdieron pronto, y, respecto de las pocas fuentes que citan presuntos dichos de Tales, no puede determinarse con certeza si tales fuentes tenían en sus manos o bien escritos de Tales o bien fuentes secundarias o si solo repetían tradiciones orales.
Aportes matemáticos
Se atribuyen a Tales varios descubrimientos matemáticos registrados en los Elementos de Euclides: la definición I. 17 y las proposiciones I. 5, I. 15, I. 26 y III. 31.
Los egipcios habían aplicado algunos de estos conocimientos para la división y parcelación de sus terrenos. Esta necesidad surgió a raíz de que el Nilo, con sus constantes crecidas, borraba las líneas divisorias de los campos de cultivo, por lo que era necesaria una manera de medir de nuevo el terreno. Mas, según los pocos datos con los que se cuenta, Tales se habría dedicado en Grecia mucho menos al espacio (a las superficies) y mucho más a las líneas y a las curvas, alcanzando así su geometría un mayor grado de complejidad y abstracción.
Aportes en el campo filosófico y cientifico
1- Nacimiento de la filosofía como pensamiento científico y racional.
Gracias a sus observaciones astronómicas,Tales pudo anticipar una gran cosecha de aceitunas que lo hizo muy rico, ya que pudo hacerse de una gran cantidad de prensas para hacer aceite.Con estas predicciones, el objetivo de Tales fue demostrar al pueblo griego los beneficiosos aspectos prácticos de la filosofía.Al medir sistemáticamente todo lo que le rodeaba, intentó desobedecer las costumbres y cuestionar las opiniones hegemónicas de la época, basadas principalmente en la mitología.
2- Surgimiento de la teología
Tales cuestiona la tradición teogónica, cosmogónica y olímpica de la época, provocando un gran salto de la teogonía -de carácter mitológico-, a la teología -de naturaleza racional- sin negar la divinidad, sino poniéndola en el debate crítico. Es en este momento cuando puede hablarse del nacimiento de la teología.
3- El agua como divinidad
Junto a Anaximandro y Anaxímenes, sus discípulos, Tales es considerado uno de los padres de la Escuela Jónica.También fueron conocidos como los “físicos”, ya que centraron sus estudios en determinar lo que era el "arché” o “arjé” (palabra acuñada mucho tiempo después por Aristoteles, o principio último, la naturaleza y origen de todas las cosas.
Buscaba algo que fuera universal y presente en todo. Este “arché” o “arjé” sería ni más ni menos que el agua, unidad indivisible.Fue considerado como principio elemental constituyente por ser límite, medio de transportación y por su capacidad de transformar su estado y forma; por ser fluida, capaz de ocupar intersticios, sutil y a la vez violenta; por cambiar, pero también sedimentar, permanecer y generar vida.Según Tales, entonces, todo fue agua en un principio. Es “lo divino”, entendido no como una identidad determinada o delimitada, sino más bien como una condición, un carácter, un “estar siendo”.4- La divinidad como un todo
Se le atribuye a Tales el concepto de “Panta plere theon”, que significa “todo está lleno de lo divino”, en un término mucho más amplio que el actual (de un único dios).
El concepto se podría explicar de esta forma: porque existe lo divino –entendido como algo inteligible, eterno y necesario- se puede entonces hablar de un todo.
Junto a Anaximandro y Anaxímenes, sus discípulos, Tales es considerado uno de los padres de la Escuela Jónica.También fueron conocidos como los “físicos”, ya que centraron sus estudios en determinar lo que era el "arché” o “arjé” (palabra acuñada mucho tiempo después por Aristoteles, o principio último, la naturaleza y origen de todas las cosas.
Buscaba algo que fuera universal y presente en todo. Este “arché” o “arjé” sería ni más ni menos que el agua, unidad indivisible.Fue considerado como principio elemental constituyente por ser límite, medio de transportación y por su capacidad de transformar su estado y forma; por ser fluida, capaz de ocupar intersticios, sutil y a la vez violenta; por cambiar, pero también sedimentar, permanecer y generar vida.Según Tales, entonces, todo fue agua en un principio. Es “lo divino”, entendido no como una identidad determinada o delimitada, sino más bien como una condición, un carácter, un “estar siendo”.4- La divinidad como un todo
Se le atribuye a Tales el concepto de “Panta plere theon”, que significa “todo está lleno de lo divino”, en un término mucho más amplio que el actual (de un único dios).
El concepto se podría explicar de esta forma: porque existe lo divino –entendido como algo inteligible, eterno y necesario- se puede entonces hablar de un todo.
Para Tales, aquello que es principio, por el mismo hecho de ser primero, ya lo hace divino. Afirma entonces que todo es divino o que “todo está lleno de dioses”, pero no en el entendido de muchas entidades físicas, sino como un principio que acoge a la naturaleza entera y es parte de su dinámica vital.
5- Descubrimientos astronómicos
Ya se ha dicho que Tales le dio mucha importancia al estudio de los astros; investigó solsticios y equinoccios y predijo y explicó los eclipses del sol y de la luna.
También, gracias a sus cálculos y observaciones, consideró a la luna 700 veces menor que el sol y calculó el número exacto de los días del año.
6- Aportaciones a la navegación
En esa época la astronomía era de esencial importancia para los navegantes, que se guiaban en sus travesías por la constelación de la Osa Mayor.
Tales de Mileto atrajo la atención de los hombres de mar al sugerir seguir la Osa Menor que, por ser más pequeña, podría dar mayor precisión.
Ya se ha dicho que Tales le dio mucha importancia al estudio de los astros; investigó solsticios y equinoccios y predijo y explicó los eclipses del sol y de la luna.
También, gracias a sus cálculos y observaciones, consideró a la luna 700 veces menor que el sol y calculó el número exacto de los días del año.
6- Aportaciones a la navegación
En esa época la astronomía era de esencial importancia para los navegantes, que se guiaban en sus travesías por la constelación de la Osa Mayor.
Tales de Mileto atrajo la atención de los hombres de mar al sugerir seguir la Osa Menor que, por ser más pequeña, podría dar mayor precisión.
7- Concepto de semejanza
Gracias a la observación y los cálculos, Tales introdujo el principio de relación de semejanza entre objetos, explicado en su primer teorema. Esto permitió avances mucho más rápidos en las matemáticas y la geometría.
Así, estableció criterios de semejanzas en triángulos, ángulos y lados que dieron lugar a sus teoremas. Por la relación de semejanza entre los triángulos rectángulos, y mediante la observación de la longitud de las sombras producidas por el sol, Tales pudo calcular la altura de los objetos.
Su caso práctico más relevante fue el cálculo del tamaño de las pirámides de Egipto: midiendo con una vara en la hora del día en que la sombra se proyecta perpendicularmente a la base de la cara desde la cual medía, le sumó la mitad de la longitud de una de las caras, obteniendo de esta forma la longitud total.
8- Fundó las matemáticas y la geometría griegas
Por ser el primero en demostrar sus teorías mediante el razonamiento lógico, se le considera el primer matemático de la historia. Los Teorema de Tales son fundamentales en la geometría moderna. Los más importantes son:
Todos los triángulos con ángulos iguales son iguales y sus lados son proporcionales entre sí.
Si varias líneas rectas paralelas se intersectan con líneas transversales, los segmentos que resultan serán proporcionales.
El constante estudio, observación y deducción, permitió que Tales concluyera otros razonamientos, tan precisos que siguen siendo sólidos en nuestros días:
Gracias a la observación y los cálculos, Tales introdujo el principio de relación de semejanza entre objetos, explicado en su primer teorema. Esto permitió avances mucho más rápidos en las matemáticas y la geometría.
Así, estableció criterios de semejanzas en triángulos, ángulos y lados que dieron lugar a sus teoremas. Por la relación de semejanza entre los triángulos rectángulos, y mediante la observación de la longitud de las sombras producidas por el sol, Tales pudo calcular la altura de los objetos.
Su caso práctico más relevante fue el cálculo del tamaño de las pirámides de Egipto: midiendo con una vara en la hora del día en que la sombra se proyecta perpendicularmente a la base de la cara desde la cual medía, le sumó la mitad de la longitud de una de las caras, obteniendo de esta forma la longitud total.
8- Fundó las matemáticas y la geometría griegas
Por ser el primero en demostrar sus teorías mediante el razonamiento lógico, se le considera el primer matemático de la historia. Los Teorema de Tales son fundamentales en la geometría moderna. Los más importantes son:
Todos los triángulos con ángulos iguales son iguales y sus lados son proporcionales entre sí.
Si varias líneas rectas paralelas se intersectan con líneas transversales, los segmentos que resultan serán proporcionales.
El constante estudio, observación y deducción, permitió que Tales concluyera otros razonamientos, tan precisos que siguen siendo sólidos en nuestros días:
No hay comentarios:
Publicar un comentario